Renormalization
《Statistical Physics of Fields》Mehran Kardar Chapter 4
Abstract
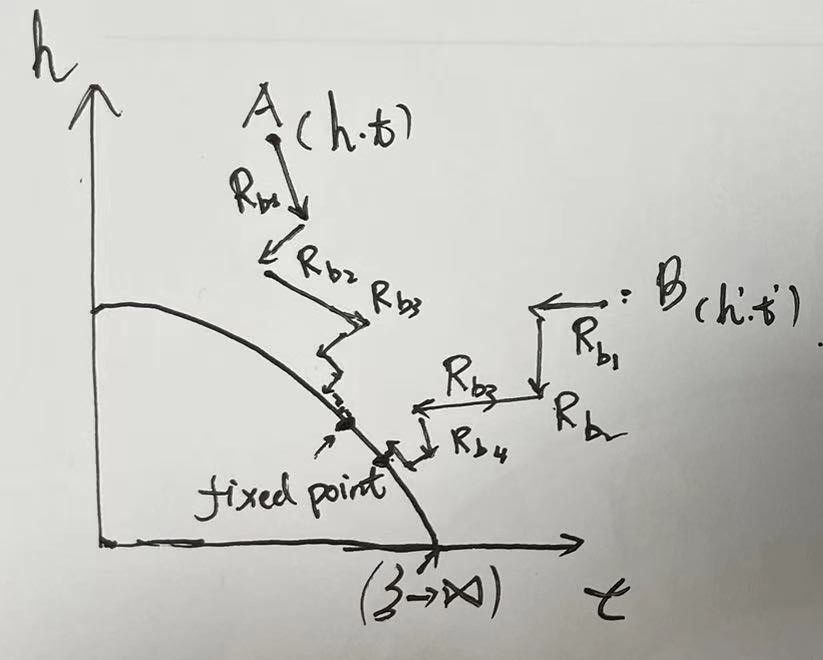
如何去寻找相变的临界指数?或许可以直接求解配分函数,但是配分函数包含了统计平衡系统的几乎全部热力学信息,只有少数体系可以严格求解;或许可以采用平均场方法,其一个不足是忽略了涨落,而从第三章讨论朗道金兹堡理论鞍点近似下对于涨落的修正中可以看出,涨落在相变时起到关键的作用。我们或许可以不去求配分函数,而是去寻找保持系统不变的对称变换$R$。在朗道朗道金兹堡理论中,自由能是由一系列参数决定的($\alpha$,$\beta$,$h$,$t$……),这个变换应当使得满足一些条件的情况下,使得远离相变的参数点不断靠近相变点,直至在无穷步后对参数点做恒等变换。这就是该变换下的不动点,找到该点就找到了相变。这个变换应当是关于空间尺度的变换,因为第三章给出了关于关联长度$\xi$的性质,即在相变时关联长度趋于无穷,如果每次变换空间尺度都改变了b,使得$\xi\rightarrow b\xi$直至不动点上 $\xi=b\xi$这说明$\xi$为零或者无穷,$\xi$无穷即相变,即这种空间尺度变换(重整化)下的不动点确为相变点。
4.4节中利用了前三节广义齐次函数的自相似性,论述这种看似粗暴的重整化变换前后不改变物理量的形式;4.5节给出如何去求解这个不动点,这个不动点是否存在的判据;4.6节,4.7节以高斯模型为例,给出严格求解,和重整化求解下的不动点参数。
4.4 The renormalization group (conceptual)
标度理论在正确预测各种指数方面的成功支持这样一种假设:系统的临界性质于是不依赖于系统在短距离内的详细细节,只依赖于长程涨落;而且这种涨落只与关联长度有关,且是自相似的。因此下面的重整化变换为了自洽,要保证宏观物理量概率分布$\exp {-\beta \mathcal{H}[\vec{m}(\mathbf{x})]}$,以及关联长度的自相似性,就是说我们要让所有构型的概率分布看起来相似,比如如下的操作:
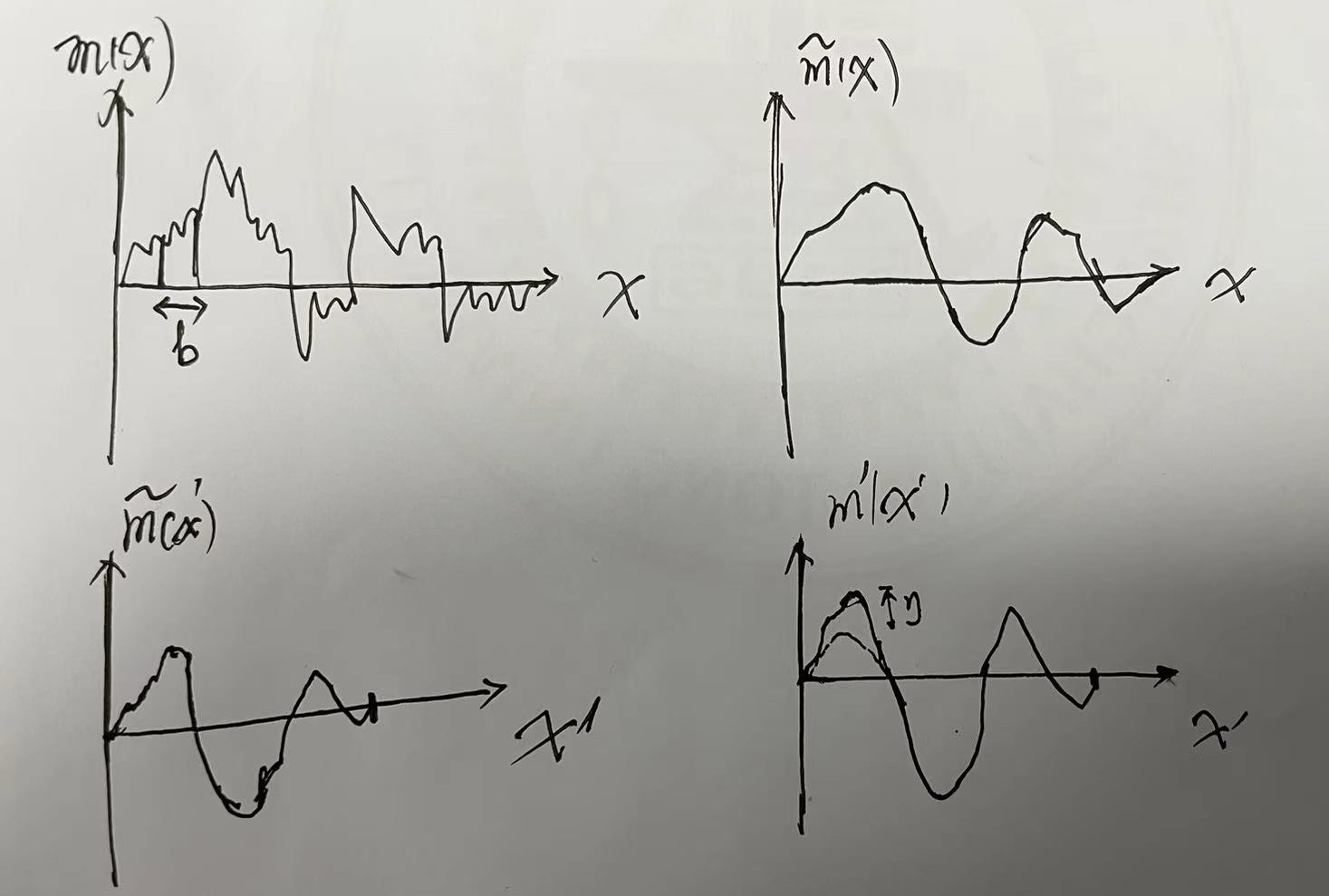
1、在b尺度内做粗粒化(coarse grain): \(m_i(\mathbf{x})=\frac{1}{b^d} \int_{\text {Cell centered at } \mathbf{x}} \mathrm{d}^d \mathbf{x}^{\prime} m_i\left(\mathbf{x}^{\prime}\right) \tag{4.27}\) 2、缩放(Rescale): \(\mathbf{x_\text{new}}=\frac{\mathbf{x_\text{old}}}{b} \tag{4.28}\) 3、重整化(renormalize),之后最终得到: \(\vec{m_\text {new }}\left(\mathbf{x_\text {new }}\right)=\frac{1}{\zeta b^d} \int_{\text {Cell centered at } b \mathbf{x_\text {new }}} \mathrm{d}^d \mathbf{x}^{\prime} \vec{m}\left(\mathbf{x}^{\prime}\right) \tag{4.29}\)
第一步,让它平滑了b倍,第二步,x轴调整让它剧烈了b’倍,第三步调整y轴让它剧烈了$\eta$倍,通过控制($\zeta$,b)保证“剧烈程度”即构型的概率分布不变,即当处于临界条件时, \(\exp {-\beta \mathcal{H}[{m_{new }}(\mathbf{x'})}] \Leftrightarrow \exp {-\beta \mathcal{H}[{m_ {old }}(\mathbf{x})}]\)
这样就保证了临界条件下的自相似性,换言之只有关联长度改变,其它物理量仍然保持着原来的广义齐次函数的形式。有所损失的是原本微观的具体函数中的弯弯绕绕,但是假设就是系统的临界性质于是不依赖于系统在短距离内的详细细节,只依赖于长程涨落,这些损失可以忽略;哈密顿量所依赖的构型在这种变换下会发生改变,但是我们不必算它,但是我们判定相变的物理量,自由能等等仍然具有价值。需要注意的是这里做的是压缩长度,压缩长度减小关联长度,远离临界点,但是不会改变重整化群的形式,即与寻找不动点无关。
我们不如假设参数空间中只有两个元素他t,h,且期望求得的重整化不动点为参数空间原点(没有常数项)。基于之前的说法,重整化变换R是某种依赖于长度b的函数,其改变了参数空间中的点($h$,$t$)到($h_{new}$,$t_{new}$),建立了两者的关联,可以做泰勒展开: \(t_b(t, h)=A(b) t+B(b) h+\cdots \\\\ h_b(t, h)=C(b) t+D(b) h+\cdots \tag{4.30}\) 朗道金兹堡理论假设的系统具有旋转对称性,即在如下的变换过后系统构型的概率分布不变,就可以认为B和D两个函数为零。 \(\beta \mathcal{H}=\beta F_0+\int \mathrm{d}^d \mathbf{x}\left[\frac{t}{2} m^2(\mathbf{x})+u m^4(\mathbf{x})+\frac{K}{2}(\nabla m)^2+\cdots-\vec{h} \cdot \vec{m}(\mathbf{x})\right] \tag{2.8}\) \(m(x) \mapsto-m(x), h \mapsto-h, t \mapsto t\)
高阶项多次迭代下可能有复杂的形式,但是对于t和h的一阶项,其满足简单的$t\left(b_1 b_2\right) \approx A\left(b_1\right) A\left(b_2\right) t \approx A\left(b_1 b_2\right) t$,并且b=1的时候为恒等变换。这表明函数A与D是简单的指数形式,即: \(t^{\prime} \equiv t_b=b^{y_t} t+\cdots \\\\ h^{\prime} \equiv h_b=b^{y_h} h+\cdots \tag{4.32}\)
在这个变换下考虑物理量,我们可以看到只要“构型的概率分布”不变,这些物理量都是自相似的,都是广义齐次函数的形式。
1、单粒子自由能$f(t,h)=kTln(Z)/N$,为了清晰一点用一个saddle point的配分函数看看形式: \(Z=\int \mathcal{D} \vec{m}(\mathbf{x}) \exp \{-\beta \mathcal{H}[\vec{m}(\mathbf{x})]\}\) \(\beta \mathcal{H}=\beta F_0+\int \mathrm{d}^d \mathbf{x}\left[\frac{t}{2} m^2(\mathbf{x})+u m^4(\mathbf{x})+\frac{K}{2}(\nabla m)^2+\cdots-\vec{h} \cdot \vec{m}(\mathbf{x})\right]\) \(Z \approx Z_{\mathrm{sp}}=\mathrm{e}^{-\beta F_0} \int \mathrm{d} \vec{m} \exp \left[-V\left(\frac{t}{2} m^2+u m^4+\cdots-\vec{h} \cdot \vec{m}\right)\right] \tag{2.10}\) \(f(t, h)=b^{-d} f\left(b^{y_t} t, b^{y_t} h\right) \tag{4.35}\)
在这个变换过程中只是他t,h发生改变,函数的形式并没有发生改变,配分函数因此也不变,只是单粒子自由能计算中要囊括一个体积因子V,重整化的过程中系统体积被压缩了$b^d$倍,把这一项加入自由能中,并最终写作广义齐次函数的形式 ($b=t^{-1 / y_t}$) :
\(f(t, h)=t^{d / y_t} f\left(1, h / t^{y_h / y_t}\right) \equiv t^{d / y_t} g_f\left(h / t^{y_h / y_t}\right) \tag{4.36}\) 对照(4.4)式,可以给出: \(f_{\text {sing }}(t, h)=|t|^{2-\alpha} g_f\left(h /|t|^{\Delta}\right) \tag{4.4}\) \(2-\alpha=d / y_t, \quad \Delta=y_h / y_t \tag{4.37}\)
2、关联长度:就是直接乘上b倍 \(\xi(t, h)=b \xi\left(b^{y_t} t, b^{y_h} h\right)=t^{-1 / y_t} \xi\left(1, h / t^{y_h / y_t}\right) \sim t^{-\nu} \tag{4.38}\) 标度率: \(\nu=1 / y_t , \quad 2-\alpha=d \nu\)
3、磁化率:
\[m(t, h)=-\frac{1}{V} \frac{\partial \ln Z(t, h)}{\partial h}=-\frac{1}{b^d V^{\prime}} \frac{\partial \ln Z^{\prime}\left(t^{\prime}, h^{\prime}\right)}{b^{-y_h} \partial h^{\prime}}=b^{y_h-d} m\left(b^{y_t} t, b^{y_h} h\right) \tag{4.39}\]标度率: \(2-\alpha-\Delta=\left(y_h-d\right) / y_t , \quad \Delta=y_h / y_t\)
所以在这种变换下,任何物理量的奇异行为都可以用广义齐次函数来描述,并且结合之前的内容,我们得到了与之前相符的标度率,还建立了其与参数$y_h$ , $y_t$的关联。
4.5 The renormalization group (formal)
现在来讨论不动点的稳定性问题,之前提到过,对于关联长度得到的不动点 $K^{\ast}$ ,有零和正无穷两个。我们回想到迭代收敛诸如牛顿法求根,根据不同的初始值选取,会收敛到不同的根。在这里,先考察重整化群的性质:命群$R_b$, 不动点$K^{\ast}$满足 $\boldsymbol{K}^{\ast}=R_s\left(\boldsymbol{K}^{\ast}\right)$,其它点$K$满足 $\boldsymbol{K}^{\prime}=R_b(\boldsymbol{K})$ 对应关联长度满足$\xi’=\xi / b$。首先,存在单位元在b=1时,第二,以$\xi$为表征量,做b1再做b2变换与做b1b2变换是一致的,做$b1b2$变换再做b3变换与做b1再做b2b3变换是一致的,第三,做了一次变换之后许多细节被抹平了,无法基于此次变换找到逆变换使得细节恢复。我们称$R_b$构成了重整化群,它是一个半群。
寻找变换对应矩阵的特征值,设$K$在$K^{\ast}$附近,我们可以写为: $K=K^{\ast}+\delta{K}$ ,其中$\delta {K}$是一个小量。把变换 ${K’}=R_b({K})$ 在$K^{\ast}$附近展开为线性项,得到:
\[{K}^{\prime}={K}^{\ast}+\delta{K'}=R_s({K})={K}^{\ast}+\mathbf{M}^{(b)} \delta {K}\]求矩阵$M$的特征值,由群结合律的性质:
\[M_b M_{b'} O=\lambda(b) \lambda(b') O=M_{b b'} O=\lambda(b b') O\]做几个M都可以结合起来,就是说特征值$\lambda$ 满足$\lambda(b^n)={\lambda(b)}^n$,并且有$\lambda(1)_i=1$ ,自然的解就是:
\[\lambda(b)_i=b^{y_i} \tag{4.46}\]这些矢量$O$被称作在不动点处的标度变换方向(scaling direction),相对应的$y_i$被称为奇异维度(anomalous dimensions)。任何一个在不动点附近的点都可以表示为:
\[K=K^*+\Sigma_i g_i O_i\]从这个点做重整化可以得到:
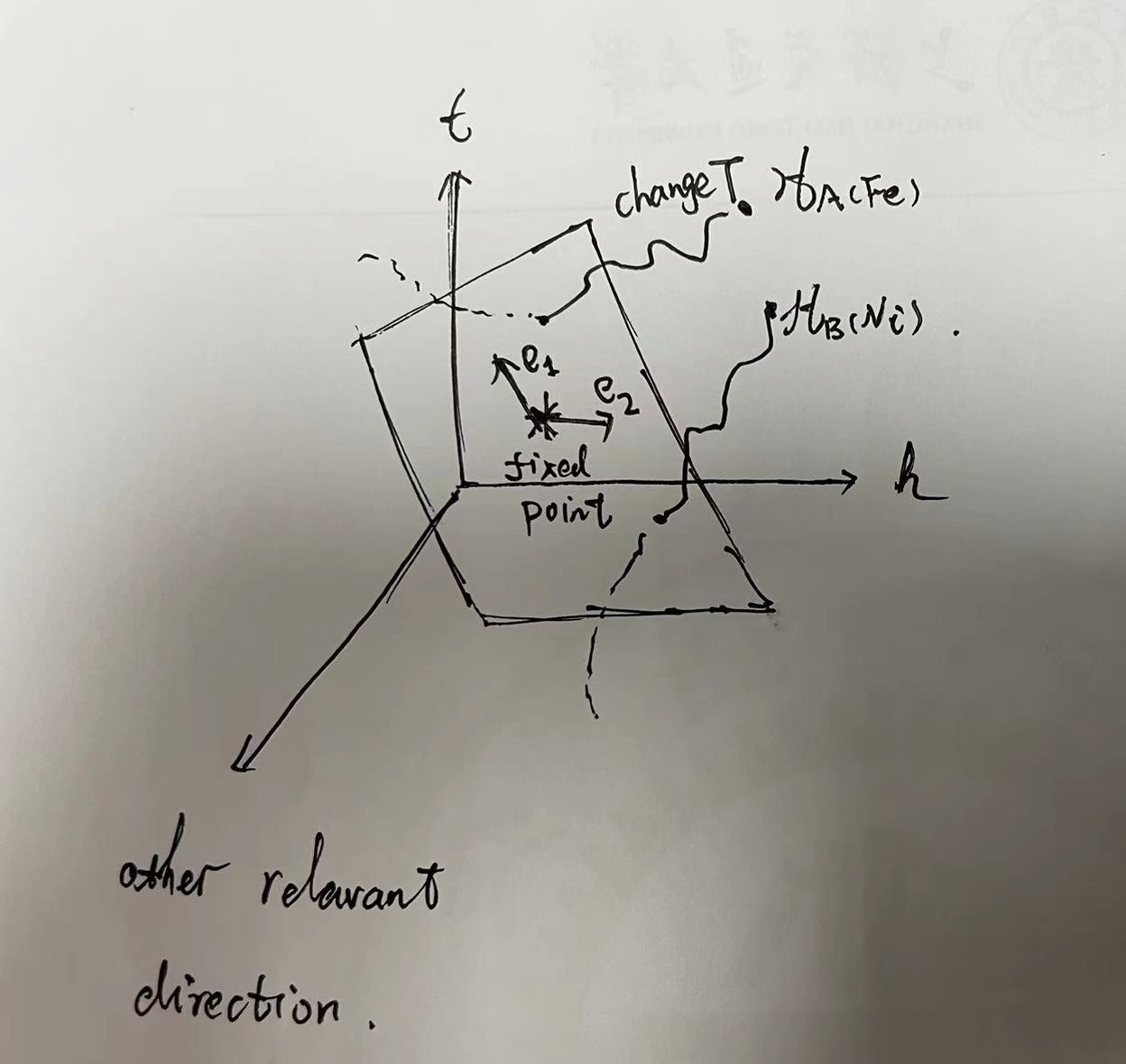
\[K'=K^*+\Sigma_i g_i b^{y_i} O_i\]其中,g是参数空间中的参量。所以我们可以看出如果本征值大于一,称为关涉本征值,相应本征矢为关涉本征矢,在粗粒化过程中标度场将被不断放大,点也不断远离不动点。如果本征值小于一,称为非关涉本征值,相应本征矢为非关涉本征矢,在粗粒化过程中标度场将被不断缩小,点也不断靠近不动点;如果本征值等于一,称为边缘本征值,相应本征矢为边缘本征矢,它依赖于系统细节。
如果e1是一个非关涉本征矢的话,沿着e1走,总会收敛到不动点;如果e2是另一个非关涉本征矢的话,沿着e2走,总会收敛到不动点。线性叠加原理告诉我们:从着e1、e2张成的平面上任意一点开始走的话,总会收敛到不动点,称这个平面为(basin of attraction of the fixed point)。如果有一个物理系统已经处在这个平面上的话,不需要对这个系统做任何实验上的改变,我们只是做了数学上的重整化操作,因为这个系统的性质在重整化前后没有任何的改变,而重整化最终得到了在不动点处无穷的关联长度,我们就可以认为物理系统在这个平面上的关联长度都是无穷的,也就是说相变发生在这个平面上。 所谓关涉本征矢就是处于这个平面之外的诸多维度,这是我们实验中在调节的东西,比如说改变温度,使得物理系统沿着改变温度所对应参数空间中的某条轨迹最终落到这个平面上,发生相变。铁有它的哈密顿量,它有许多微观自由度;镍有它的哈密顿量,它也有许多微观自由度,这些微观自由度组成了巨大的非关涉本征矢空间,全空间写作:
而当发生相变时
或者我们可以考虑无外磁场情况下的某个磁铁随温度发生的相变,这时候磁场与一堆微观自由度共用非干涉本征矢:
如果它们都落在了这个平面上,称这两种相变属于同一个普适类。就是说系统有某种微观相似性,比如由自旋相互作用的自由度主导的,具有相似的相变;或是把外磁场也考虑进来,即在外磁场不断改变下具有相似的相变规律。
Question: 一般说非关涉本征矢空间巨大而关涉本征矢最多只有两个(极少可观测量),Why?Kardar4.5: Again, other “odd” interactions,such as $m^3$ $m^5$··· , should not lead to any other relevant operators.这些项的作用是什么?
4.6 The Gaussian model (direct solution)
这一节我们直接解出高斯模型的的临界指数,下一节利用RG再做一遍。高斯模型在朗道金兹堡理论下只保留到m的平方项:
\[Z=\int \mathcal{D} \vec{m}(\mathbf{x}) \exp \{-\beta \mathcal{H}[\vec{m}(\mathbf{x})]\}\] \[\beta \mathcal{H}=\beta F_0+\int \mathrm{d}^d \mathbf{x}\left[\frac{t}{2} m^2(\mathbf{x})+\frac{K}{2}(\nabla m)^2+\cdots-\vec{h} \cdot \vec{m}(\mathbf{x})\right]\]做傅里叶变换:
\[\vec{m}(\mathbf{q})=\int \mathrm{d}^d \mathbf{x} \mathrm{e}^{\mathrm{i} \mathbf{q} \cdot \mathbf{x}} \vec{m}(\mathbf{x}) \\\\ \vec{m}(\mathbf{x})=\sum_{\mathbf{q}} \frac{\mathrm{e}^{-\mathrm{i} \mathbf{q} \cdot \mathbf{x}}}{V} \vec{m}(\mathbf{q})=\int \frac{\mathrm{d}^d \mathbf{q}}{(2 \pi)^d} \mathrm{e}^{-\mathrm{i} \mathbf{q} \cdot \mathbf{x}} \vec{m}(\mathbf{q}) \tag{4.50}\]最终得到:
\[Z=\prod_{\mathbf{q}} V^{-n / 2} \int \mathrm{d} \vec{m}(\mathbf{q}) \exp \left[-\frac{t+K q^2+L q^4+\cdots}{2 V}|m(\mathbf{q})|^2+\vec{h} \cdot \vec{m}(\mathbf{q}=0)\right] \tag{4.53}\]自由能为:
\[f(t, h)=-\frac{\ln Z}{V}=\frac{n}{2} \int_{B Z} \frac{\mathrm{d}^d \mathbf{q}}{(2 \pi)^d} \ln \left(t+K q^2+L q^4+\cdots\right)-\frac{h^2}{2 t}\]可以从自由能的奇异部分当中确定临界指数,q都是平方项,在有限q的情况下ln函数不会发散,自由能不是奇异的。而当t趋近于零的时候则是感兴趣的情况,第一项在q在零附近积分时会是奇异的。我们截取自由能的奇异部分即第二项,以及第一项积分靠近原点的部分,假设积分上限为较小的$\Lambda$,是一个球。
\[f_{\text {sing }}(t, h)=\frac{n}{2} K_d \int_0^{\Lambda} \mathrm{d} q q^{d-1} \ln \left(t+K q^2+L q^4+\cdots\right)-\frac{h^2}{2 t} \tag{4.57}\]然而书上进一步的变量代换仍然不很直观,不妨先计算热容,是自由能对温度的两阶导数,除去了ln项留下都是指数项,再恢复到自由能中,从而得到标度率。
从而标度率为:
\[\alpha_{+}=2-d / 2, \quad \Delta=1 / 2+d / 4 \tag{4.60}\]4.7 The Gaussian model (renormalization group)
重新回到此式,不做高斯积分。 \(Z \sim \int \mathcal{D} \vec{m}(\mathbf{q}) \exp \left[-\int_0^{\Lambda} \frac{\mathrm{d}^d \mathbf{q}}{(2 \pi)^d}\left(\frac{t+K q^2+L q^4+\cdots}{2}\right)|m(\mathbf{q})|^2+\vec{h} \cdot \vec{m}(\mathbf{0})\right]\)
1、粗粒化,消除 a < x < ba 尺度上的波动类似于消除动量空间中$\Lambda$/b < q < $\Lambda$的傅立叶模式。这就是说,实空间中抹去的是震荡剧烈的细节,对应动量空间中抹去的是高动量的部分。也就是说通过做一个截断,我们可以把动量分成两个子空间,直接把高动量的部分积分积掉,这一部分自由能肯定不存在奇异性,不会改变构型的概率分布。幸运的是在高斯模型下面这两个子空间互不影响,可以直接把截断部分扔在一边。
\[Z=\int \mathcal{D} \tilde{\vec{m}}\left(\mathbf{q}^{<}\right) \int \mathcal{D} \vec{\sigma}\left(\mathbf{q}^{>}\right) \mathrm{e}^{-\beta \mathcal{H}[\tilde{\tilde{m}}, \vec{\sigma}]} \tag{4.63}\] \[\begin{aligned} Z & \sim \exp \left[-\frac{n}{2} V \int_{\Lambda / b}^{\Lambda} \frac{\mathrm{d}^d \mathbf{q}}{(2 \pi)^d} \ln \left(t+K q^2+L q^4+\cdots\right)\right] \times \int \mathcal{D} \tilde{\vec{m}}\left(\mathbf{q}^{<}\right) \\\\ & \times \exp \left[-\int_0^{\Lambda / b} \frac{\mathrm{d}^d \mathbf{q}}{(2 \pi)^d}\left(\frac{t+K q^2+L q^4+\cdots}{2}\right)|\tilde{m}(\mathbf{q})|^2+\vec{h} \cdot \tilde{\vec{m}}(\mathbf{0})\right] . \end{aligned} \tag{4.64}\]2、3步,变换q尺度$\mathbf{q}^{\prime}=b \mathbf{q}$ ;变换m尺度$\vec{m}^{\prime}\left(\mathbf{q}^{\prime}\right)=\tilde{\vec{m}}\left(\mathbf{q}^{\prime}\right) / z$,得到:
\[\begin{aligned} Z= & \mathrm{e}^{-V \delta f_b(t)} \times \int \mathcal{D} \vec{m}^{\prime}\left(\mathbf{q}^{\prime}\right) \times \exp \left[-\int_0^{\Lambda} \frac{\mathrm{d}^d \mathbf{q}^{\prime}}{(2 \pi)^d} b^{-d} z^2\right. \\\\ & \left.\times\left(\frac{t+K b^{-2} q^{\prime 2}+L b^{-4} q^{\prime 4}+\cdots}{2}\right)\left|m^{\prime}\left(\mathbf{q}^{\prime}\right)\right|^2+z \vec{h} \cdot \vec{m}^{\prime}(\mathbf{0})\right] \end{aligned} \tag{4.66}\]寻找不动点,重整化变换前后系统构型的概率分布不变,即配分函数不变,将此配分函数与最初的配分函数对照,可以得到参数的关系式:
\[t^{\prime}=z^2 b^{-d} t \\\\ h^{\prime}=z h \\\\ K^{\prime}=z^2 b^{-d-2} K \\\\ L^{\prime}=z^2 b^{-d-4} L \\\\\]可以看到预料中的t=h=0为不动点。还需要保证余下的参数也处于不动点,设置参数z可以达到这一点,$z=b^{1+d / 2}$,因此可以得到重整化变换的关系式: \(\begin{aligned} & y_t=2 \\\\ & y_h=1+d / 2 \end{aligned}\)
利用4.4节得到的诸多标度关系可以最终求解这个重整化变换,得到广义齐次函数形式,其与4.6节严格求解的结果一致。
\[\begin{aligned} & \nu=1 / y_t=1 / 2, \\\\ & \Delta=\frac{y_h}{y_t}=\frac{1+d / 2}{2}=\frac{1}{2}+\frac{d}{4} \\\\ & \alpha=2-d \nu=2-d / 2 \end{aligned}\]在高斯模型中,关涉本征矢就是t和h了,且存在大量的非关涉本征矢对应于m的多阶导数,通过设置参数z,使得K做恒等变换,也同时将大量的非关涉本征矢迭代到零。同时,如果对哈密顿量做一个微扰,使得有更多的关涉本征矢参与其中(比如加上$m^3$,$m^4$这些项),通过设置参数z仍然可以确定更高阶关涉本征矢对应的y值,比如说$y_4=4-d$ ;$y_6=6-2 d$ 。第四阶的m只在小于等于三维的情况下为关涉本征矢,第六阶的m只在一、二维为关涉本征矢。所以说引入更高阶的微扰大量的宏观物理量也作为非关涉本征矢,只有领头的几阶才会在我们所需的维度上可供调整。
Example Ising
1-D Ising 严格求解没有相变,平均场得到在$2J$时发生相变。
重整化操作就是把2个自旋粗粒化为一个“自旋”,再丢掉所有偶数格点上的自旋,再对配分函数引入参数A使得配分函数不变。无外场下1-D Ising 配分函数为(J=1):
\[\begin{aligned} Z(T)= & \sum \exp \left(\frac{1}{k T} \sum_{i=1}^N s_i s_{i+1}\right)=\sum_{\text {odd }} \sum_{\text {even }} \exp \left(\frac{1}{k T} \sum_{i=1}^N s_i s_{i+1}\right) \\\\ = & \sum_{odd} \sum_{even} \exp \left(\frac{1}{k T} s_{even}\left(s_{odd}+s_{odd}\right)\right) \end{aligned}\]丢掉偶部分,就是先把偶的部分求和求掉,代入$s_{even}$为正负一,求得:
\[Z_i=2 \cosh \left(\frac{1}{k T}\left(s_{i-1}+s_{i+1}\right)\right)\]做rescaling就是把格点i-1,i+1,变为i,i+1,宏观物理量只有温度T,在此变换下变为了T’。左边的式子是基于重整化之前的哈密顿量,它的配分函数在重整化之后的形式,右边是重整化体系的哈密顿量对应的配分函数,这个新的配分函数需要待定系数进行如下猜测。为了保证配分函数的形式相等,联立重整化前与重整化后的配分函数,对任意的i,有:
\[2 \cosh \left(\frac{1}{k T}\left(s_{i}+s_{i+1}\right)=\exp \left(A+\frac{1}{k T^{\prime}} s_{i} s_{i+1}\right)\right.\]代入s的值(1,1)(1,-1)(-1,1)(-1,-1),总共得到两个方程,并进行化简:
\(\begin{aligned} & 2 \cosh 2 \frac{1}{k T}=\exp \left(A+\frac{1}{k T^{\prime}}\right) \\\\ & 2=\exp \left(A-\frac{1}{k T^{\prime}}\right) \end{aligned}\) \(\frac{1}{k T^{\prime}}=\frac{1}{2} \log \left(\cosh \left(2 \frac{1}{k T}\right)\right)\)
这就是重整化变换前后参量温度的函数关系,借此便可以找到温度的不动点,只有一个点,零温的时候。温度为0这一点并不是系统的相变点。但却是一维模型中的一个平凡的满足自相似性的点,符合对一维中不存在相变的预期。
2-D Ising 严格解2.3J,平均场解4J,重整化做如下操作:
求和掉所有的黑色块,余下白色的块,旋转45度得到自相似的体系,再做rescaling,renormalization等操作。基于原本的哈密顿量配分函数所作重整化得到的形式,同一维类似,也是代入黑色格点的自旋数值,把黑色格点求和求出来,得到余下白色格点的求和:
\[Z\left(K_1, N\right)=\sum_{w h i t e} \cdots 2 \cosh \left(K_1\left(s_{i, 1}+s_{i, 2}+s_{i, 3}+s_{i, 4}\right)\right) \cdots\]另一方面重整化之后的哈密顿量对应的配分函数具有未知的形式,但是它应当在每个i处与先前的配分函数相等。先前的配分函数对于自旋的不同取值,会有三种情况,而如果仍然想一维情况一样假设两个参量无法做联立。由于重整化后的哈密顿量是未知的,不如大胆假设其引入了次近邻相互作用,以及四自旋相互作用,从而用四个参量来表示配分函数:
\[Z’=\exp \left(K_0^{\prime}+\frac{K_1^{\prime}}{2}\left(s_{i, 1} s_{i, 2}+s_{i, 1} s_{i, 4}+s_{i, 2} s_{i, 3}+s_{i, 3} s_{i, 4}\right)+K_2^{\prime}\left(s_{i, 1} s_{i, 3}+s_{i, 2} s_{i, 4}\right)+K_3^{\prime}\left(s_{i, 1} s_{i, 2} s_{i, 3} s_{i, 4}\right)\right)\]对于自旋的不同取值做联立:
\[\begin{gathered} 2 \cosh (4 K_1)=\exp \left(2 a+b+\frac{1}{2} c+\frac{1}{2} d\right) \ldots \ldots \ldots \ldots(4+; 4-) \\\\ 2 \cosh (2 K_1)=\exp \left(-\frac{1}{2} c+\frac{1}{2} d\right) \ldots \ldots \ldots \ldots(3+1-; 3-1+) \\\\ 2=\exp \left(-2 a+b+\frac{1}{2} c+\frac{1}{2} d\right) \ldots \ldots \ldots(+,-,+,-;-,+,-,+) \\\\ 2=\exp \left(-b+\frac{1}{2} c+\frac{1}{2} d\right) \ldots \ldots \ldots(+,+,-,-;-,-,+,+) \end{gathered}\]最终得到了关于所需的$K_1$的递推关系式:
\[K_1^{(s+1)}=\frac{3}{8} \log \left(\cosh 4 K_1^{(s)}\right)\]这个变换关系具有一个非零的不动点$K_1^*=0.507$ ,$K_1$的定义为$1/kT$,相变温度位于1.97$(J=1)$处,与严格解对比,效果比平均场优秀。