t-J Model in High-Temperature Superconductor
Small Survey
Abstract
t-J模型是铜氧化物高温超导机理研究的重要模型。本调研先介绍t-J模型的物理来源,高温超导研究的历史与困境,再拓展课上讲的Zhang-Rice单态,利用理论说明为什么t-J模型适合研究铜氧化物高温超导;接着介绍t-J模型模拟上的困境与进展,最后会以一篇最新的文献研究具体分析t-J模型在判断高温超导相中的作用。
Introduction
t-J模型是一种量子自旋模型[1.Assa Auerbach],用于研究凝聚态物理中的强关联电子系统。在数学上,t-J模型可以由Huabbrad模型导出,其考虑了Huabbard模型对于单占据态的作用,通过投影算符至单占据态上,t-J模型有效的聚焦于电子的自旋自由度和它们在晶格上的运动。它的哈密顿量主要包含两个部分:自旋-自旋相互作用项和电子跃迁项。自旋-自旋相互作用项描述了电子之间的相互作用,而电子跃迁项描述了电子在晶格上的运动,具体来说,其哈密顿量为:
\[\hat{H}=-t \sum_{\langle i j\rangle, \sigma}\left(c_{i \sigma}^{\dagger} c_{j \sigma}+\text { h.c. }\right)+J \sum_{\langle i j\rangle}\left(\mathbf{S}_i \cdot \mathbf{S}_j-\frac{n_i n_j}{4}\right) \tag{1}\]如果我们要研究系统中的输运性质,我们可以聚焦于t:电子跃迁项,它表示了电子在晶格上从一个位置跃迁到另一个位置的概率振幅, 体现了系统的动力学行为。而交换耦合常数J可以描述交换相互作用。事实上,这是一种超交换相互作用,超交换相互作用导致了一种称为“自旋配对”的现象,或者说是形成超导体的关键的库珀对,在比如铜氧化物为代表的高温超导体中,这种交换相互作用被认为是超导性的重要机制之一。
我们另外关注的一个名词“高温超导体”,也具有漫长的研究历史[2.wikipedia]。在实验上,已经发现了多种高温超导体,一个代表就是铜氧高温超导体,其超导转变温度可以处于90K-150K左右。自1987年发现CuO2铜氧面为主要结构单元的超导体称之为第一类高温超导家族,而2008年以后出现了以铁砷层(FeAs)或者铁硒层(FeSe)为主要结构单元的超导材料,称第二类高温超导家族。
然而,形成高温超导的机理十分复杂,其中一个核心问题是判断什么相互作用导致了超导的电子配对,是借助某些玻色子形成配对呢,还是直接配对的方式。现在的状况是理论预言繁多,却难以严格或是覆盖全部。一些配对方法已经有了共识,比如导致超导态d-波配对的媒介是反铁磁涨落。而近年来对于体系对称性的研究超越了朗道的经典理论,即序参量微扰发散预示着体系自发对称性破缺,而是说体系形成了一种非费米液体态,对于这种态的研究可以帮助揭示高温超导的机理。
t-J模型描述高温铜氧超导的Zhang-Rice 单态[3][4]
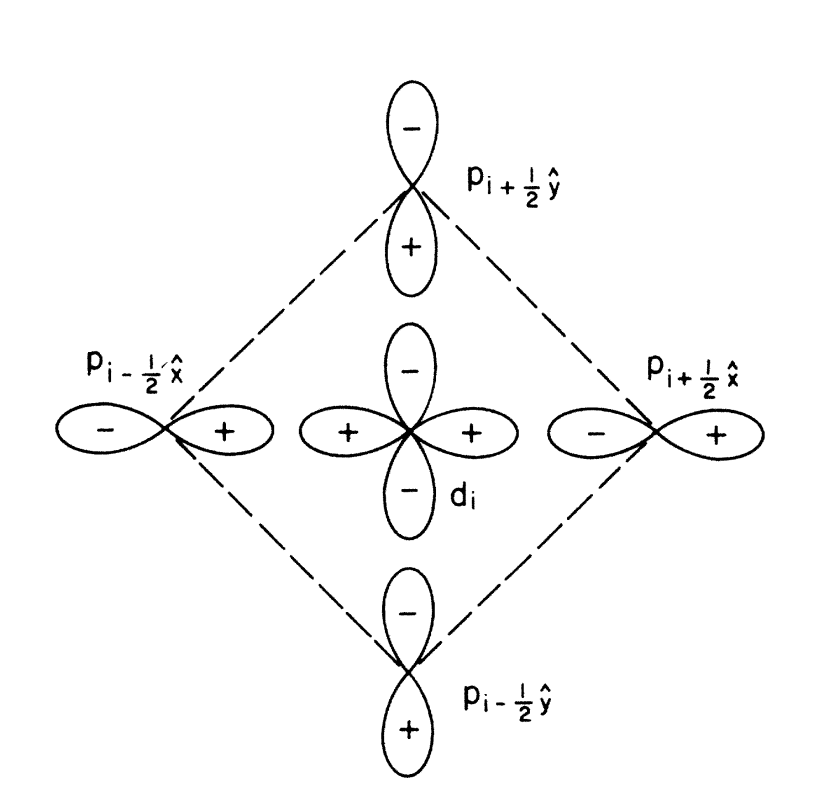
Zhang-Rice 单态我们在课上已经提到过了,就是因为铜氧化物典型的2D铜氧面,掺入到铜氧化物中的空穴会在氧上,并且它与铜氧化物中的氧形成的对称态会和铜空穴形成一个自旋为零的单态,称之为Zhang-Rice单态。那么这样假设之后张富春和Rice就认为铜氧化物超导材料的低能有效模型为t-J模型,论证如下,我们还是考虑一个铜氧平面,描述体系的哈密顿量为:
\[\begin{aligned} H= & \sum_{i, \sigma} \epsilon_d d_{i \sigma}^{\dagger} d_{i \sigma}+\sum_{l, \sigma} \epsilon_p p_{l \sigma}^{\dagger} p_{l \sigma} +U \sum_i d_{i \uparrow}^{\dagger} d_{i \uparrow} d_{i \uparrow}^{\dagger} d_{i \downarrow}+H^{\prime} \\\\ H^{\prime}= & \sum_{i, \sigma} \sum_{l \in\{i\}} V_{i l} d_{i \sigma}^{\dagger} p_{l \sigma}+\text { H.c. } \\\\ \end{aligned} \tag{2}\]对于一个铜氧平面体系来说,氧作用的是$p^6$电子,第二项描述了这些电子;铜作用的是$d^{10}$电子,第一项与U项描述了这些电子。总体描述了氧的p空穴,铜的d空穴以及铜的库伦相互作用。$H^{\prime}$项描述了铜氧交换相互作用。比如我们考虑实际的$La_{2}CuO_{4}$。氧没有空穴,铜有一个,铜全部处于单占据态。这种单据态能够发生的虚拟跃迁就是铜铜单据之间的超交换,对应反铁磁,显然是t-J模型。
现在我们考虑$CuO_{2}$多了空穴,放在哪里呢?如果放在铜上面,那氧还是没有参与的机会,相当于原来铜配对的氧现在配对的氧被消除了一些,那还是t-J模型。如果放在氧上面,这样一来铜氧就各有空穴可以发生交换相互作用,不过要注意的一点是反对称的交换作用是不被允许的,应为计算下来这样的Hopping能量要远小于这些局域态自己的上下上下能级差;另一点是由于中间隔了一个氧,铜的局域态之间并不正交,需要做一些上的处理。
这么做之后就可以计算这个Hopping了:
\[t_{i j}=\sum_{\{w\}}\left\langle\psi_i^{-} d_{j \sigma}\left|H^{\prime}\right| w\right\rangle\left\langle w\left|H^{\prime}\right|\left(\psi_j^{-} d_{i \sigma}\right)^{+}\right\rangle / \Delta E_w \tag{3}\]其中$\psi$就是为了正交性新构造的铜氧态,$\omega$遍历这些铜氧态的各个中间态,E就是两态能量差,一般对于双据是$\epsilon_p-U$。费米黄金规则表明Hopping能量可以用Hopping哈密顿量二阶微扰展开,对应就是上式,所有数据都具备。结论t约为-1.5V,对应反铁磁相互作用,构造合理。而构造的新的$\psi$态与等效Hopping哈密顿量为:
\[\begin{aligned} \psi_i^{ \pm}= &(1 / \sqrt{2})\left(\phi_{i \uparrow} d_{i \downarrow} \pm \phi_{i \downarrow} d_{i \uparrow}\right) \\\\ H_t= &\sum_{i \neq j, \sigma} t_{i j}\left(\psi_j^{-} d_{i \sigma}\right)^{+} \psi_i^{-} d_{j \sigma} \\\\ \end{aligned} \tag{4}\]其中$\phi$为正交化后的p,对应氧空穴,d对应铜空穴。这个式子的物理含义就是$\psi$代表了铜氧化物的在氧上的空穴与氧形成的单态。而Hopping哈密顿量就代表了每产生一个铜上面的d空穴,就会消灭一个这样的单态,这就是d上面空穴的空态,就是说d上面空穴被两个空态的投影算符(这个单态)一夹,不是你有就是我有,对应的哈密顿量为:
\[H_t=\sum_{i \neq j, \sigma} t_{i j}\left(1-n_{i,-\sigma}\right) d_{i \sigma}^{\dagger} d_{j \sigma}\left(1-n_{j,-\sigma}\right) \tag{5}\]这就是t-J模型的哈密顿量。
t-J模型模拟高温超导计算上的困境与进展 [5][6]
t-J 模型的主要困难在于其中的 Gutzwiller投影算符,因为Zhang-Rice态说明了同一格点上不能同时占据两个电子,很难构建这样一种可以求解的波函数。但是可以构造一种Gutzwiller试探波函数:
\[|\left.\Psi_G\right\rangle=\prod_i\left(1-(1-g) n_{i \uparrow} n_{i \downarrow}\right)\left|\Psi_0\right\rangle \tag{6}\]Gutzwiller方法是上世纪六十年代提出的,和本文没有太大关系,只是知道关键是参数g抑制了双据态。而我们使用的处理t-J模型的主要方法是重整化平均场理论。它基于Gutzwiller近似的波函数,本质上仍然是一种变分近似。所谓平均场就是指所得到的Gutzwiller波函数可以计算其变分能量,变分能量的关键假定参数可以用重整化参数来表示,而重整化参数在初始构型和结束构型都对应单据态的情况下是容易写出的。接着就可以使用通常的平均场方法,得到超导序参量的关联。目前重整化平均场理论广泛应用在不局限于t-J模型的强关联体系中,而关于t-J模型预言高温超导机理,Gutzwiller方法也应用于超导强度,考虑次近邻相互作用t-J模型下求解超导相的过程,以及考虑最近邻格点之间的相互作用的t-J模型求解超导相的过程。使用重整化平均场理论计算对于特定材料实验结果的比较和变分蒙特卡洛的模拟相比几乎一致。
在数值模拟上,量子蒙特卡洛结果虽然好但还是得考虑符号问题,求解t-J模型基态问题以DMRG的MPS态为代表的张量网络仍然是相当好的方法。不过近年来也有发明一种GMERA方法,它结合了Grassman代数和张量网络。Grassman代数可以有效地解决费米子的统计问题,而张量网络我们主要做的是矩阵的缩并。把矩阵的缩并简化为Grassman数的重排,我们就不必关注全局性质,而是每两两Grassman数操作后的结果了。相较DMRG,GMERA解决t-J模型可以更加关注于发生配对自发对称破缺的高温超导模型,已经有利用GMERA计算t-J模型具有争议的基态性质的研究。
最新进展:Enhanced Intertwined Spin and Charge Orders in the 𝑡–𝐽 Model in a Small 𝐽 Case [7]
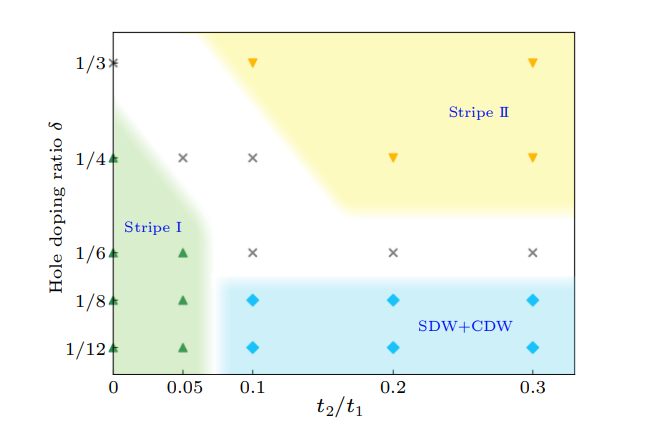
2023年有许多t-J模型或是高温超导机制的研究,但很多要不是发展t-J模型各种形式,要不是就是高温超导的诸多性质:在CDW, PDW方面。这篇二月份的文章主要讲的是考虑次近邻情况下t-J模型的超导,还分析了其中一种新的SDW + CDW态的性质。与高温超导相关的是他们对于与高温超导相关的intertwined orders,以及一些其它序参量的分析。结论是在较深的Mott趋于会存在增强的intertwined orders以及受到限制的超导性质。
在凝聚态物理中,”interwined orders”(交织的序)指的是多个序参量(order parameter)之间的相互依赖和相互影响。高温超导研究的“interwined orders”指的是电荷密度波和超导序参量之间的相互作用。在某些铜氧化物超导体中,除了存在超导性,还存在着电荷密度波序参量,两者会相互竞争。比较深的Mott趋于指的是J较小的情况,t-J模型哈密顿量为: \(H=-\sum_{[i j] \sigma} t_{i j} P_{\mathrm{G}}\left(c_{i \sigma}^{\dagger} c_{j \sigma}+\text { h.c. }\right) P_{\mathrm{G}}+\sum_{[i j]} J_{i j}\left(\boldsymbol{S}_i \cdot \boldsymbol{S}_j-\frac{n_i n_j}{4}\right) \tag{7}\)
其中$P_G$就是之前提到过的Gutzwiller投影算符。其中t有两种,最近邻称$t_1$,次紧邻称$t_2$。在接下来的模拟中恒定$t_1/J=10$。数值模拟方法是有限维DMRG,48格点,由六腿晶格组成(six-leg lattice)。x方向周期边界条件,y方向开放边界条件,得到的相图如下:
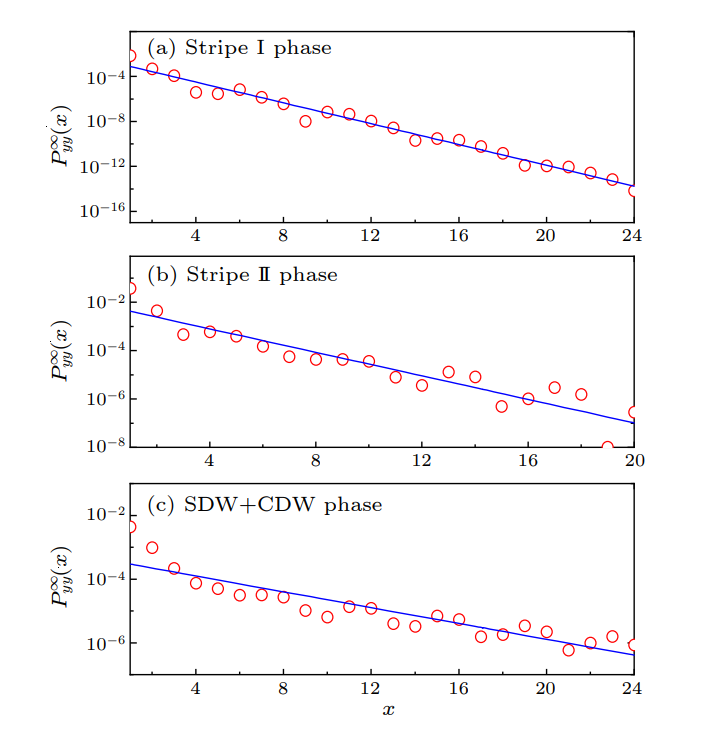
右边这张图说明的是超导相不存在,超导就是配对,如果配对强度指数衰减的话,那可以说超导相不存在。因此可以定义配对关联强度P。([8.Bruss.Chap18]BCS平均场方法给出了定义配对关联强度的方法) :
\[\begin{aligned} P_{\alpha \beta}\left(x, y_0\right)= &\left\langle\Delta_\alpha^{\dagger}\left(x_0, y_0\right) \Delta_\beta\left(x_0+x, y_0\right)\right\rangle \\\\ \Delta_\alpha^{\dagger}(x, y)= &\frac{1}{\sqrt{2}}\left[c_{(x, y) \uparrow}^{\dagger} c_{(x, y)+\alpha \downarrow}^{\dagger}-c_{(x, y) \downarrow}^{\dagger} c_{(x, y)+\alpha \uparrow}^{\dagger}\right] \end{aligned} \tag{8}\]可以从右图发现在三个相中间确实存在者指数衰减的配对关联强度,因此三个相都没有超导存在,下面要说明存在两个条纹相和一个CDW+SDW相。
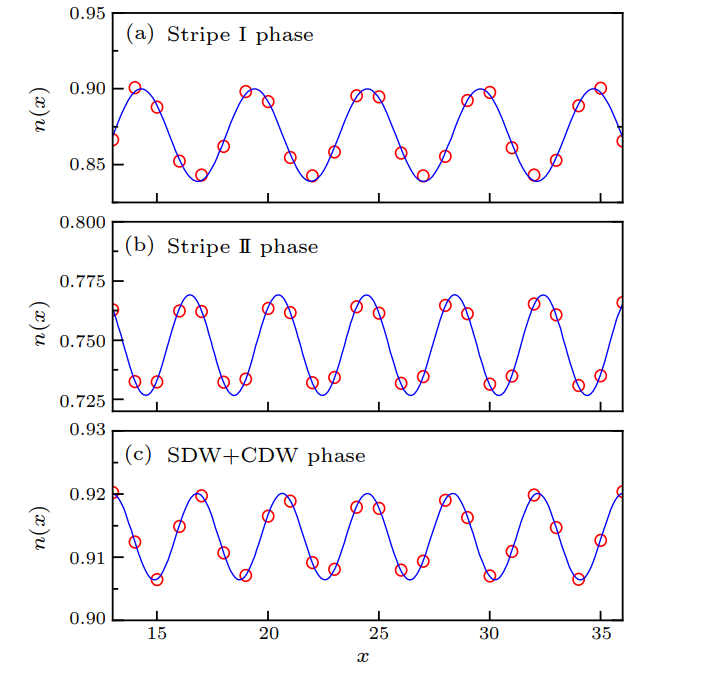
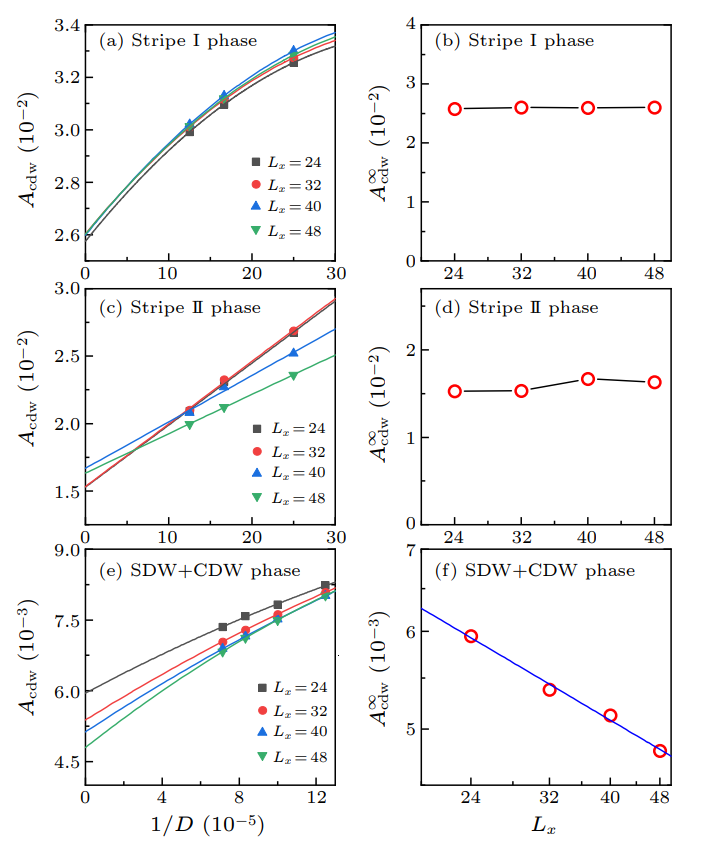
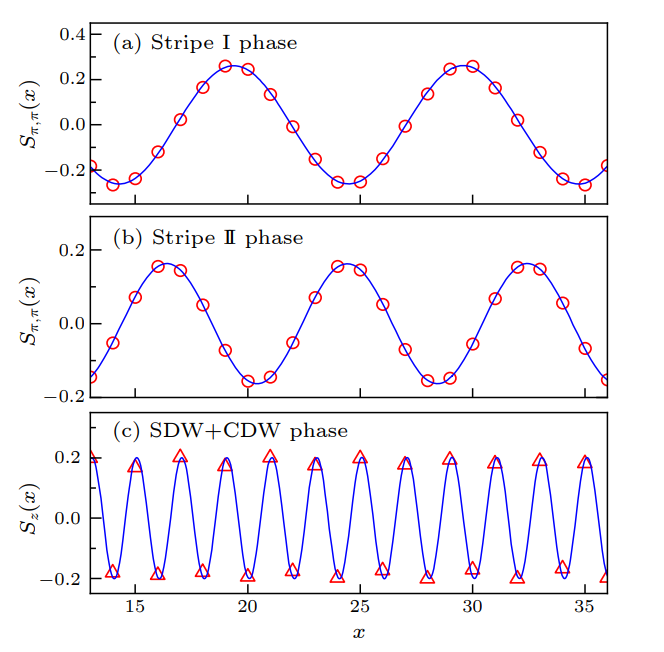
这两张图是CDW分布以及CDW幅度。根据电荷密度波理论,统计电荷密度可以由波动解给出:
\[n(x)=n_0+A_{\mathrm{cdw}} \cos \left(Q_{\mathrm{cdw}} x+\phi_{\mathrm{cdw}}\right) \tag{9}\]其中n电荷密度,Q波长倒数,A振幅都可以从左边这张图上读出。而模拟得到左边这张图则是统计电荷密度,DMRG可以给出。右边这张图就是由此得到的振幅与张量网络中张量之间的连接数D,以及格点数的关联。由左图至少看出三个相都有CDW结构在里面,如果是纯的CDW结构,就如同stripe对应于右图的上面两张是尺寸无关的,而CDW+SDW态结合使得最后一张图在双对数坐标系下线性,即随尺寸指数衰减的CDW振幅,说明第三相中CDW只是局域的序,收到SDW牵制。
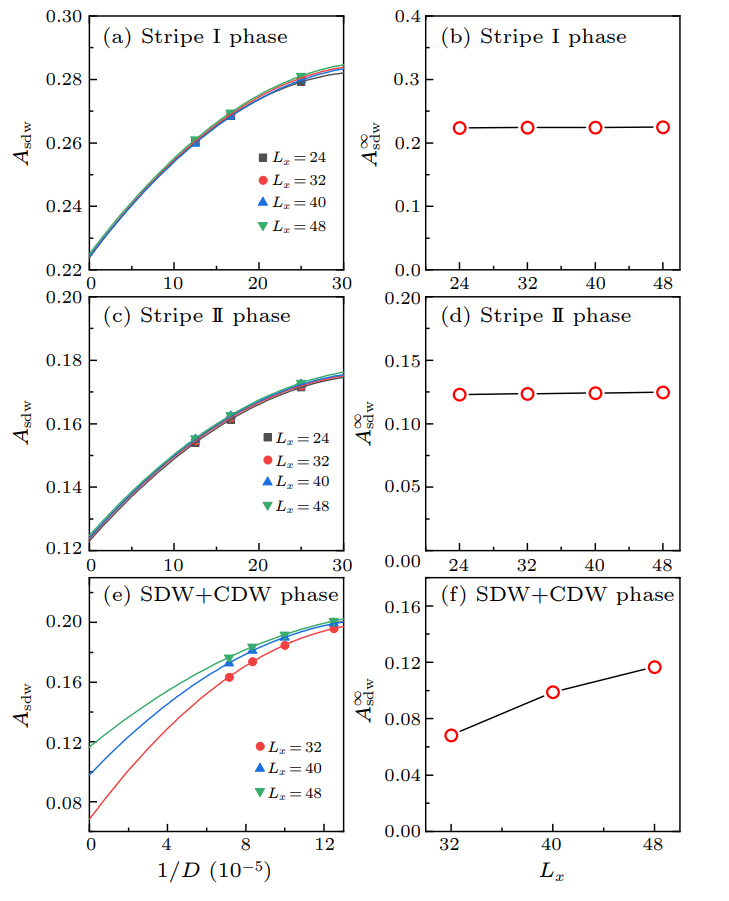
这两张图是SDW分布以及SDW幅度。取的是沿z方向的自旋,自旋上与自旋下的差作为分布的y指标。同样的我们可以假设波动解的分布。SDW独立存在于前两相,第三相随着系统尺寸,SDW振幅增加,体现了一个更加稳定的SDW序,也是SDW,CDW共同作用的结果。本文设定的t/J=10已经是较深的Mott区域了,可以看到考虑了次紧邻相互作用的t-J模型在这个区域不存在超导相,而是由条纹相以及CDW+SDW相组成。
REF
[1] Interacting Electrons and Quantum Magnetism》Assa Auerbach
[2] High-Temperature Superconductivity. Wikipedia.[website](https://en.wikipedia.org/wiki/High-temperature_superconductivity)
[3]t-J model then and now: A personal perspective from the pioneering times.Jozef Spalek.[Arxiv](https://arxiv.org/abs/0706.4236v1)
[4]Effective Hamiltonian for the superconducting Cu oxides. F.C.Zhang and T. M.Rice, Phys.Rev.B 37, 3759(1988).
[5]重整化平均场理论及其在铜氧化物高温超导材料中的应用.易伟柱,奚文杰,陈伟强.Low.Temp.Phys.Lett.42,0059(2020)
[6]Grassmann代数与张量网络——研究强关联费米模型的崭新数值方法[J].娄捷. 物理, 2017, 46(7): 439-445.
[7]Enhanced Intertwined Spin and Charge Orders in the 𝑡–𝐽 Model in a Small 𝐽 Case. Yu Zhang, Jiawei Mei, and Weiqiang Chen 2023 Chin. Phys. Lett. 40 037401. [8]《Many-Body Theory in Condensed Matter Physics—— An Introduction》Henrik Bruus and Karsten Flensberg