Half-Odd Integer Spin Chains
《Interacting Electrons and Quantum Magnetism》Assa Auerbach Chapter 5
Abatract
拥有半整数自旋的粒子波函数,围绕任一轴旋转360度后,其波函数需要增添一个负号。发生在三维空间的这种旋转是平凡的,而低维空间中的旋转将对能带产生影响。更进一步,在十一章,我们会利用半经典的自旋波函数理论再次诠释;在十四章,我们会讨论整数自旋的情况。在本节,我们会先讨论低维条件下旋转前后的两态的能量,并发现在热力学极限下总会存在一个激发态,其与基态之间没有带隙 (gapless), 随后将举例讨论这种现象带来的物理效应。笔者在文中会涉及一些对称性的内容,尚且生疏,有错误之处还请指正。
Half-Odd Integer Spin AntiHeisenberg Chain
Lieb, Schultz and Mattis Theorem [3]
Consider the Heisenberg antiferromagnet (J>0) on a chain,
\[\mathcal{H}=J \sum_{j=1}^{\mathcal{N}} \mathbf{S} _ {j} \cdot \mathbf{S} _ {j+1}+J \mathbf{S}_{\mathcal{N}} \cdot \mathbf{S}_1 \tag{5.38}\]where $\mathcal{N}$ is even. For half-odd integeger spins e.g., S=1/2,3/2,…, there exists an excited state with energy that vanishes as $\mathcal{N}\rightarrow\infty$.
Q: 为什么$\left|\Psi_1 \right\rangle$ 不能也是基态?Def: 基态 $\left|\Psi_0 \right\rangle$ 激发态 $\left|\Psi_1 \right\rangle$ 旋转算符 $\mathcal{O}$ $\left|\Psi_1 \right\rangle \equiv \mathcal{O}\left|\Psi_0 \right\rangle$
Def: 算符U: $U_x \mathbf{S} _ j U_x^{-1}=\mathbf{S} _ {j+1}$ 其与哈密顿量对易 $\left[\mathcal{H}, U_x\right]=0$
A:我们讨论的体系是一维反铁磁海森堡链,总粒子数是偶数。也就是说,为了满足上一节的反铁磁基态条件,在一维链上自动的分为了两个子格,且子格中格点数相同。这样一来,利用Marshall Theorem 5.2,5.4, 基态是非简并的,且总自旋为零。
即证:$\left\langle\Psi_1 \mid \Psi_0\right\rangle=0$ 以及 $\lim _{\mathcal{N} \rightarrow \infty}\left[\left\langle\Psi_1|\mathcal{H}| \Psi_1\right\rangle-E_0\right] \rightarrow 0 $
我们巧妙地选取旋转算符以使得第一个所证式成立:
\[\mathcal{O}=\exp \left(i \frac{2 \pi}{\mathcal{N}} \sum_{j=1}^{\mathcal{N}} j S_j^z\right) \tag{5.39}\]由于H与U对易,$U\left|\Psi_0\right\rangle$ 亦为相差了一个相位的基态,即所证式:
\[\begin{aligned} \left\langle\Psi_0 \mid \Psi_1\right\rangle & =\left\langle\Psi_0 \mid \mathcal{O} \Psi_0\right\rangle \\\\ & =\left\langle\Psi_0\left|U_x \mathcal{O} U_x^{-1}\right| \Psi_0\right\rangle \\\\ \end{aligned} \tag{5.46}\] \[\begin{aligned} U_x \mathcal{O} U_x^{-1} & = U_x \exp \left(i \frac{2 \pi}{\mathcal{N}} \sum_{j=1}^{\mathcal{N}} j S_j^z\right) U_x^{-1}=\exp \left(i \frac{2 \pi}{\mathcal{N}} \sum_{j=1}^{\mathcal{N-1}} j S_{j+1}^z\right)\cdot \exp \left(i \frac{2 \pi}{\mathcal{N}} \mathcal{N}S_1\right) \\\\ & =\exp \left(i \frac{2 \pi}{\mathcal{N}} \sum_{j=0}^{\mathcal{N-1}} (j+1) S_{j+1}^z\right)\cdot \exp \left(-i \frac{2 \pi}{\mathcal{N}} \sum_{j=1}^{\mathcal{N}} S_{j}^z\right) \cdot \exp \left(i \frac{2 \pi}{\mathcal{N}} \mathcal{N}S_1\right) \\\\ & = \mathcal{O} \cdot \exp \left(-i \frac{2 \pi}{\mathcal{N}} S_{total}^z\right) \cdot \exp \left(i 2 \pi S_1\right) \\\\ \end{aligned}\]我们已知:
\[\exp \left(-i \frac{2 \pi}{\mathcal{N}} S_{total}^z\right) \left| \Psi_0\right\rangle=\left| \Psi_0\right\rangle (基态为总自旋为零的态Marshall 5.2) \tag{5.48}\]并且对于上式最后一项,整数的自旋取+1;而半整数的自旋取-1;因此对于半整数的自旋而言:
\[\begin{aligned} \left\langle\Psi_0 \mid \Psi_1\right\rangle & =\left\langle\Psi_0\left|U_x \mathcal{O} U_x^{-1}\right| \Psi_0\right\rangle \\\\ & =\left\langle\Psi_0 \mid -\mathcal{O} \Psi_0\right\rangle \\\\ &=-\left\langle\Psi_0 \mid \Psi_1\right\rangle =0 \\\\ \end{aligned} \tag{5.51}\]通过这个证明我们可以发现选取旋转算符的巧妙之处。事实上,对于具有U(1)旋转对称性的哈密顿量而言,具有非简并的基态说明了基态也具有U1旋转对称性,这体现在普通的“旋转” (5.48) 不会改变基态, 我们需要定义一个新的与格点序号有关的“旋转”,以使得其作用在基态上增添一个负号(5.51),这样定义了$\mathcal{O}$。
不解:本质上是$\mathcal{O}$的什么对称性,符合了半整数自旋的什么性质,才添了一个负号?
对于第二个所证式而言,
\[\begin{aligned} \left\langle\Psi_{1}|H| \Psi_{1}\right\rangle & =\left\langle\Psi_{0}\left|\mathcal{O}^{-1} H\mathcal{O}\right| \Psi_{0}\right\rangle \\\\ & =\left\langle H_{z}\right\rangle+\left\langle\exp \left(-i \frac{2 \pi}{N} \sum_{j=1}^{N} j S_{j}^{z}\right)\right| \sum_{j=1}^{N} S_{j}^{x} S_{j+1}^{x} + J S_{N}^{x} \cdot S_{1}^{x}\left|\exp \left(i \frac{2 \pi}{N} \sum_{i=1}^{N} j S_{j}^{z}\right)\right\rangle \\\\ & + \left\langle\exp \left(-i \frac{2 \pi}{N} \sum_{j=1}^{N} j S_{j}^{z}\right)\right|\sum_{j=1}^{N} S_{j}^{y} S_{j+1}^{y} + J S_{N}^{y} \cdot S_{1}^{y}\left|\exp \left(i \frac{2 \pi}{N} \sum_{i=1}^{N} j S_{j}^{z}\right)\right\rangle \\\\ \end{aligned}\]利用对易关系:
\[[S^i,S^j]=i\epsilon_{ijk}S^k\]得到对于求和中的第j项,对易关系不为零的项为:
\[\exp \left(-i \frac{2 \pi}{N} (j-1) S_{j-1}^{z}\right)\exp \left(-i \frac{2 \pi}{N} j S_{j}^{z}\right) \exp \left(-i \frac{2 \pi}{N} (j+1) S_{j+1}^{z}\right)( S_{j}^{x} S_{j+1}^{x} +S_{j}^{y} S_{j+1}^{y} +S_{j-1}^{x} S_{j}^{x} +S_{j-1}^{y} S_{j}^{y} )\]级数展开指数项,利用:$[(S^{z})^{n},S^x]=iS^y(n奇);S^x(n偶)$;
\[\begin{aligned} \exp \left(-i \frac{2 \pi}{N} j S_{j}^{z}\right) S_{j}^{x} & = \sum_{n}\frac{(-i\frac{2 \pi}{N} j)^n}{n!} S_{j}^{x}\\\\ & =S_{j}^{x}\exp \left(-i \frac{2 \pi}{N} j S_{j}^{z}\right)+ \sum_{奇}\frac{(-\frac{2 \pi}{N} j)^n}{n!} S_{j}^{y}+\sum_{偶}\frac{(-\frac{2 \pi}{N} j)^n}{n!} S_{j}^{x} \\\\ &=S_{j}^{x}\exp \left(-i \frac{2 \pi}{N} j S_{j}^{z}\right)-sin(\frac{2 \pi}{N} j)S_{j}^{y}+cos(\frac{2 \pi}{N} j)S_{j}^{x} \\\\ \end{aligned}\]而$\exp \left(-i \frac{2 \pi}{N} j S_{j}^{z}\right)\exp \left(-i \frac{2 \pi}{N} (j+1) S_{j+1}^{z}\right) (S_{j}^{x} S_{j+1}^{x}+S_{j}^{y} S_{j+1}^{y})$包含了比如项$S_{j}^{x} S_{j+1}^{y}$前的系数为:
\[-cos(\frac{2 \pi}{N} j)sin(\frac{2 \pi}{N} (j+1))+sin(\frac{2 \pi}{N} j)cos(\frac{2 \pi}{N} (j+1)=sin(\frac{2 \pi}{N} )\]这样就消去了j,把前面所有过程总结起来,得到了(5.52)
\[\left\langle\Psi_{1}|\mathcal{H}| \Psi_{1}\right\rangle=E_{0} +\left\langle\Psi_{0}\right|[\cos (2 \pi / \mathcal{N})-1] \sum_{j=1}^{\mathcal{N}}\left(S_{j}^{x} S_{j+1}^{x}+S_{j}^{y} S_{j+1}^{y}\right) +\sin (2 \pi / \mathcal{N}) \sum_{j=1}^{\mathcal{N}}\left(S_{j}^{x} S_{j+1}^{y}-S_{j}^{y} S_{j+1}^{x}\right)\left|\Psi_{0}\right\rangle\]最后一项的求和号里面其实就是$[S_{total}^z,H]$由于基态是自旋单态,这一项为零,并利用不等式(从定义式可以推知,但过繁?):
\[\left\langle S_{j}^{x} S_{j+1}^{x}+S_{j}^{y} S_{j+1}^{y}\right\rangle \leq S^{2}\]并把(5.52)式中的余弦保留到最小阶,就最终得到了:
\[\left\langle\Psi_{1}|\mathcal{H}| \Psi_{1}\right\rangle-E_{0} \leq \frac{2 \pi^{2} J S^{2}}{\mathcal{N}}+\mathcal{O}\left(\mathcal{N}^{-3} \right) \tag{5.55}\]在粒子数趋于无穷时旋转后的激发态与基态能量趋于相同,带隙合拢,这样就完成了证明。
Majumdar-Gosh Model
我们回顾刚才发现的规律,发现正因为旋转720度之后半整数自旋才会回复原来位置,在旋转360度之后的态,与基态,属于同一组,属于新的“基态”,也事实上的分裂了基态,产生了一个较低的第一激发态,从而破坏了格点的对称性。比如Majumdar-Gosh Model (Assa. Chap8) [6],其考虑了次近邻的相互作用,其中$\alpha$是一个可调参数。
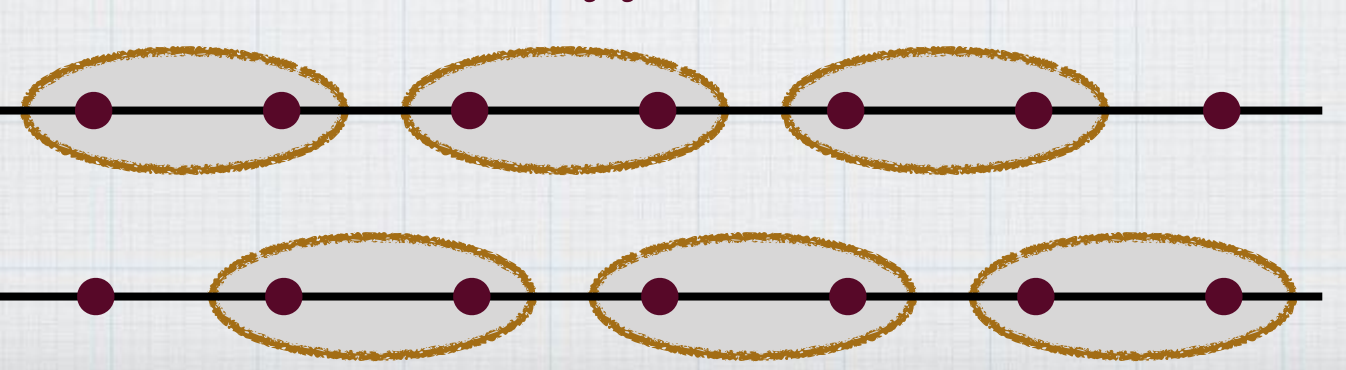
\[H=\frac{1}{2} J \sum_{i=1}^{N} \sigma_{i} \cdot \sigma_{i+1}+\frac{1}{2} J \alpha \sum_{i=1}^{N} \sigma_{i} \cdot \sigma_{i+2}\]基态是可以求解的,如下左图所示,称这样的两两组合的基态为“dimer configuration”,其中每一个“dimer configuration” 的态为自旋单态.
下面两张图是四粒子的能量随$\alpha$的变化图,以及N较大时的上下两带能量,当粒子数趋于无穷时,带隙合拢,而此时基态每个自旋的能量为($\alpha=1/2$) $-3/4 J$。
Magnon Excitations
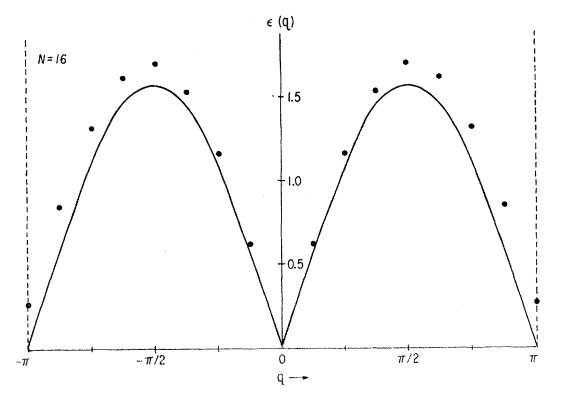
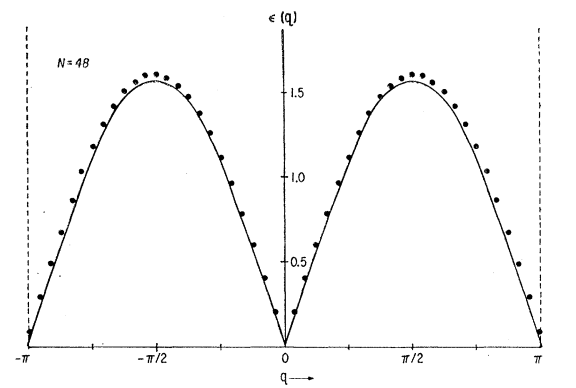
1962年,Jacques des cloizeaux ang J. J. Pearsont [2] 解析的求解了无穷一维最近邻海森堡模型,能量如下图所示,其包括了一组简并的能带,能带是没有带隙的,而在动量空间k=0与k=$\pi$处,这些激发(magnon excitations)趋于零,具体为(Assa. Chap11) $\omega_{\mathbf{k}}=(\pi / 2)|\sin k|$
我们不太严谨的利用一种半经典手段来说明这件事:一个粒子自旋的改变事实上是与周围最近邻粒子自旋的交换作用,如果我们把自旋视作一个随时间连续变化的量,并且大部分自旋是沿着z轴的,那么它应当具有“运动方程”,“Equations of motion”,对于p位的格点,粒子自旋(角动量)的变化来自于磁力矩,磁矩正比与该格点的自旋量子数,”磁场“来源于最近邻格点的自旋:
\[\begin{aligned} \hbar \frac{d \mathbf{S} _ {\mathbf{p}}}{d t} & =\mu_{\boldsymbol{p}} \times \mathbf{B} _ {\mathrm{p}} \\\\ & =\left(\frac{-g \mu_{B}}{\hbar}\right) \cdot S_{p} \times B_{p} \\\\ & =\left(\frac{2 J}{\hbar}\right) S_{p} \times\left(S_{p-1}+S_{p+1}\right) \\\\ \end{aligned}\]对于自旋近似沿z轴,化简可以得到:
\[\begin{aligned} \frac{d S_{2 p}^{x}}{d t} & =\left(\frac{2 J S}{\hbar}\right) \cdot\left[-2 S_{2 p}^{y}-\left(S_{2 p-1}^{y}+S_{2 p+1}^{y}\right)\right] \\\\ \frac{d S_{2 p}^{y}}{d t} & =\left(\frac{-2 J S}{\hbar}\right) \cdot\left[-2 S_{2 p}^{x}-\left(S_{2 p-1}^{x}+S_{2 p+1}^{x}\right)\right] \\\\ \frac{d S_{2 p+1}^{x}}{d t} & =\left(\frac{2 J S}{\hbar}\right) \cdot\left[2 S_{2 p+1}^{y}+\left(S_{2 p}^{y}+S_{2 p+2}^{y}\right)\right] \\\\ \frac{d S_{2 p+1}^{y}}{d t} & =\left(\frac{-2 J S}{\hbar}\right) \cdot\left[2 S_{2 p+1}^{x}+\left(S_{2 p}^{x}+S_{2 p+2}^{x}\right)\right] \\\\ \end{aligned}\]存在正负号的差异,是因为反铁磁状态导致的自旋有正负。这式子我们可以假设行波解来求解,用系数行列式为零来求解参数能量,并最终得到:
\[\hbar \omega=4 J S|\sin (\mathrm{ka})|\]与半整数自旋不同,在Chap.15,我们会讨论整数自旋的情况,能隙存在,称为Haldane Gap。这里的讨论并不能给出整数自旋的情况,因为对于整数自旋证明1不能给出任何信息。 之所以存在能隙是因为拓扑贝瑞相之间的量子干涉,当我们学习15.1节时会专门的了解。
More general LSM theorem (略)
LSM理论自1961年之后又有长足的发展,即半整数自旋如何得到非简并无带隙的基态?具体来说是把限制条件放宽到了多类更广泛的具有某种对称性的哈密顿量上,以及在二维等条件下的情况。近年来LSM帮助理解一些不同维度、不同对称性的拓扑相。
我们下面尝试举例说明一个更加一般的Lieb, Schultz and Mattis Theorem:即只要哈密顿量满足 平移不变性与时间反演对称性,对于无穷长的半整数自旋的反铁磁一维链,要么它简并无带隙,要么它非简并有带隙 [5]。
Consider a quantum spin chain with and a short-ranged Hamiltonian that is invariant under translation and time-reversal. Then it can never be the case that the corresponding infinite volume ground state is unique and accompanied by a nonzero gap.
时间反演下:$S\rightarrow-S$,时间反演算符T可以写作幺正算符与复共轭算符的乘积,我们利用半整数自旋体系中只有y方向的泡利矩阵为复数,可以得到自旋体系中时间反演算符的形式,其中$\eta$为一个相位,K为复共轭算符。
\[\hat{T}=\eta \exp \left(-\frac{i \pi \hat{S} _ {y}}{\hbar}\right) \hat{K},\]易推知对于每个半整数自旋 $T^2=-1I$ 从而得到对于时间反演不变的哈密顿量,$\left|\Psi_0 \right\rangle$ 与 $T\left|\Psi_0 \right\rangle$ 简并(克拉默简并)。接下来我们从单个自旋拓展至无限长的自旋1/2链,$T^2=(-1)^JI$,其中$J=\sum_{i}J_i$ 代表了对每个格点处自旋的标记求和,半整数自旋标记为1,整数自旋标记为0。
我们回到之前的Majumdar-Gosh Model的dimer states。如果对于一个无穷链,从中在第j个位置左侧切断这根链取这条链的右半段,对于不同的两个dimer configuration,一个有完整的dimer,一个裸露出来一个自旋,尽管它们仍然是无穷链。对于这两种不同的“构型”,我们引入第二个标记,在i处,$(-1)^{L_i}$ 对于dimer $L_i=0$,对于裸露自旋 $L_i=1$。
定理:$L_i=J_i+L_{i+1}$
对于满足平移对称性,时间反演对称性的链,我们假设它是有带隙的,非简并的。我们取两条带,仍然在i处切断,由于具有平移对称性,这与另一条在i+1处切断没有区别,$L_i=L_{i+1}+J_i=L_{i+1} \rightarrow J_i=0$说明是整数自旋,矛盾。
REF
[1]《Interacting Electrons and Quantum Magnetism》Assa Auerbach
[2] Spin-Wave Spectrum of the Antiferromagnetic Linear Chain, Jacques des Cloizeaux and J. J. Pearson, Phys. Rev. 128, 2131 (1962)
[3] Two soluble models of an antiferromagnetic chain Author links open overlay panel, Elliott Lieb, Theodore Schultz, Daniel Mattis, Annals of Physics,Volume 16, Issue 3 (1961)
[4] 姚老师的笔记
[5] Lieb-Schultz-Mattis type theorem in quantum spin chains without continuous symmetry. lecture notes. Hal Tasaki.(https://www.youtube.com/watch?v=OFB9bGu8E38),
[6] On Next Nearest Neighbor Interaction in Linear Chain. I Chanchal K. Majumdar, Dipan K. Ghosh. J. Math. Phys. 10, 1388 (1969);