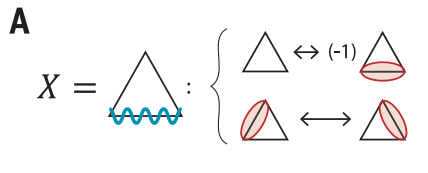Introduction to Quantum Spin Liquid

Abatract

---

  量子自旋液体(Quantum Spin Liquid, QSL)是一种由量子自旋相互作用而形成特殊的物质相，其特点是长程量子纠缠、分段激发以及不存在普通磁序。本文从三角格点中的阻挫引入QSL的概念，再给出一种利用RVB态描述QSL的方法，从而揭示其重要的物理内涵。接着概述QSL目前的发展、应用前景及其挑战并给出一篇文献作为例证。QSL有广阔的研究前景，笔者作为初学者有所不足烦请指正。

What is Quantum Spin Liquid ?

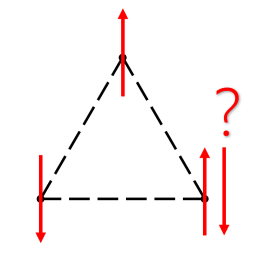
Ising Triangle Ground State

  我们考虑三角格点中的基态问题，假设其是反铁磁相互作用的伊辛自旋，(Wannier ,1950)[1]求解了这个著名的问题。对于一个三角格点而言，为了满足能量最低原理，前两个自旋可以倾向于反铁磁排列，但是这导致了第三个自旋既不能向上，也不能向下（下左图）；最终最低的能量状态应该为三个自旋呈120度夹角排列 (6种排列方式)。

   在多体问题中考虑这种情况，如果一个三角格点就有6种基态，可以预估，基态简并度随着格点数目指数级增加（右上图）。这些自旋都无法呈反铁磁态排列，因为那样能量并非最低，而是呈QSL态排列。事实上的系统不会处于任何的这些基态上，而是因为系统与环境的微扰在这些指数级的基态上不断浮动。更进一步，最近邻格点任然有形成反铁磁排列的倾向，但是它（比如图中的绿色标记）只能和某一个形成短暂的反铁磁排列(Singlet),并不断因为浮动交替与它形成singlet的对象，从而让这个系统由一对一对不断变化的singlet组成，这就如同液体一样，得名量子自旋液体。
  这种效应带来的阻挫就是QSL研究的重要物理意义之一。此外，分数激发也用来描述QSL态。QSL态难以以序参量表述，比如磁化率都是大量浮动的，无法从任何一个局部入手——我们需要一种超越经典朗道相变理论的方法，这可能需要应用拓扑序。我们也看到电子和电子的配对，这使得单电子近似的能带理论失效，这些都带来了QSL态的物理意义。

Resonating valence bond State (RVB)

  我们可以利用RVB态（共振价键态）描述上述的短暂的反铁磁排列。(Assa. Chap8) [2]描述了这一过程。

  上图是RVB态的两个例子，为了描述这一对一对的情况，不能用不同的自旋相干态——那对应了单粒子情况，而是要利用Schwinger bosons代数，其同时激发了两个自旋，一上一下，对应了其中的一个singlet。其数学描述为：

\[\begin{aligned} S^x+i S^y & =a^{\dagger} b, \\ S^x-i S^y & =b^{\dagger} a \\ S^z & =\frac{1}{2}\left(a^{\dagger} a-b^{\dagger} b\right) . \end{aligned} \tag{1}\]

   RVB态为：

\[|\alpha\rangle=\prod_{(i j)}\left(a_i^{\dagger} b_j^{\dagger}-b_i^{\dagger} a_j^{\dagger}\right)|0\rangle \tag{2}\]

  其中，S为原来的自旋，由S构造的a,b算符满足自旋相关的代数规则。我们称a产生算符作用产生一个自旋向上态，b产生算符作用产生一个自旋向下态。这样$\alpha$态就成为了这样一对一对的共振价键态：

\[\prod_{(i, j)}\left(\left|\uparrow_{i}\downarrow_j\right\rangle-\left|\downarrow_i \uparrow_j\right\rangle\right) \tag{3}\]

   RVB态能够揭示出QSL许多的性质。比如在升温的过程中，有一些格点处的自旋会脱离原本的singlet产生一个spinon,又比如可以在RVB态中发现电荷分数化现象，等等。

Application of Quantum Spin Liquid

  2017年的综述文章《Quantum Spin Liquid States》[3]给了许多关于量子自旋液体前沿与研究现状的介绍。比如人们正在探索一些超越RVB假设的自旋液体态。正如之前所述，RVB态的一个典型特征是基态的singlet，现在发现在自旋为1的体系下由于自旋轨道的耦合作用这种singlet可能会被打破；另外就是对高于1/2自旋系统的探索：对于其它自旋引入了一组满足普适的对称群的代数形式，来重写自旋相互作用算符，比如S=1的自旋液体满足的U(1)或$Z_2$对称性就与S=1/2的不同。近来量子自旋液体经常与拓扑序和量子相变相关联，反映QSL态的一些全局的拓扑特征。在实验上，人们也在尝试从不同材料中官场QSL态。一个重要的指标是无局域的磁有序，在2003年被发现，之后在kagome，quaitriangler等晶格材料上都有所发现。
  计算复杂性一直是阻碍QSL模拟的挑战。近年来比如MPS方法构造的tensor简化了诸如DMRG在内的数值模拟算法，但是仍然只能较少的格点，而这对于浮动的QSL态来说显得不足。在实验上，有许多与理论不符之处：比如外加磁场在一个有着spinion费米面的U(1)对称性的QSL态上导致的热霍尔效应，尚未被实验所验证。
  最后我们通过一篇文献更进一步了解QSL的研究现状。《Probing topological spin liquids on a programmable quantum simulator》[4]这篇文章搭建了一个量子模拟系统，在上面观察到了QSL态的信息，作者认为所搭建的模拟体系是可控的，可以可控的观察物质的拓扑性质，以及最近兴起的拓扑保护的量子信息。

在kagome晶格上的里德堡原子

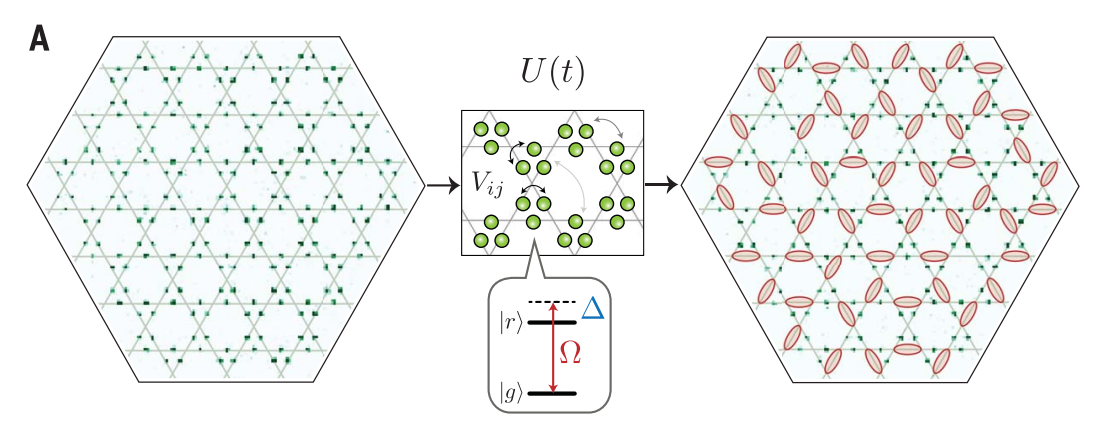
  该体系将里德堡原子置于kagome晶格的中间（如图），让它们在时间演化下形成VBS态。里德堡原子具有“里德堡屏蔽(Rydberg blockade)”效应，相邻的里德堡原子间存在互斥的作用力，通过调整原子属性——里德堡半径，可以将VBS态的一个dimer的范围局域在恰好一个vertex(一个三角的顶点)上。
  该体系的相互作用能量依赖于双光子跃迁效应(two-photon optical transition)。原子基态为图中的g态，里德堡态为图中的r态，通过双光子跃迁机制，存在一个虚拟能级，使得两态之间可以相互作用，对应两个能量图中的$\Omega$与$\Delta$。此二者之比为可调参数。总哈密顿量就可以写作：

\[\begin{aligned} \frac{H}{\hbar}= & \frac{\Omega(t)}{2} \sum_i \sigma_i^x-\Delta(t) \sum_i n_i +\sum_{i<j} V_{i j} n_i n_j \\\\ n_i= & \left|r_i\right\rangle\left\langle r_i\right| \\\\ \sigma_i^x= & \left|g_i\right\rangle\left\langle r_i|+| r_i\right\rangle\left\langle g_i\right| \\\\ \end{aligned} \tag{4}\]

  相互作用V项代表了里德堡原子之间的相互作用，相互作用$\Omega$项与相互作用$\Delta$项代表了时间演化下的双光子跃迁效应。在一个vertex上可以存在多个连接的dimer，通过调整$\Omega$与$\Delta$之比为4左右的时候，实验上看到一个vertex上连接的有且仅有一个dimer。

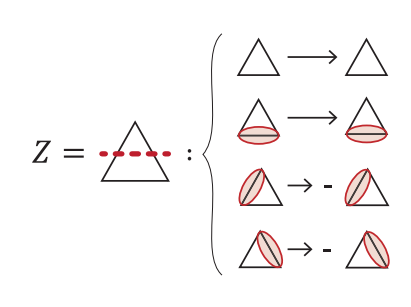
“拓扑弦” ：Z和X类型

  toric code model在2003年由Kitaev提出，可以实现容错拓扑量子计算。此模型中对应toric code model有两个算符，一是对角算子(diagonal operator)Z，二是非对角算符(off-diagonal)X, 定义如下：

  其中Z算符代表了体系对称性，简单来说，kagome晶格每个交叉点延伸出的四条线，上面有一个dimer，Z就乘上-1.反之为1。因此对于包含一个格点的封闭线(loop)，理想的Z均值(1vertex-1dimer)为-1，这可以相似的推广到更大的loop上，并模拟不同的$\Omega$与$\Delta$之比对Z的变化。而X算符可以在$\Delta$为零时由Z算符时间演化相似变换得来，这也是模拟得到X算符数值的方法。X算符代表了不同VBS态之间的对应特定loop之间的外积，反映了loop连接的dimer态之间的耦合强弱。
   我们之所以要考虑Z与X算符是因为QSL态不存在局域磁序，需要另找拓扑不变量。而toric code model说明了存在这么一个精确解，对应了无能隙的量子自选液体相，对应了不同体系的拓扑不变量。现在问题是我们定义的Z与X为什么是好的，能够找到QSL态。
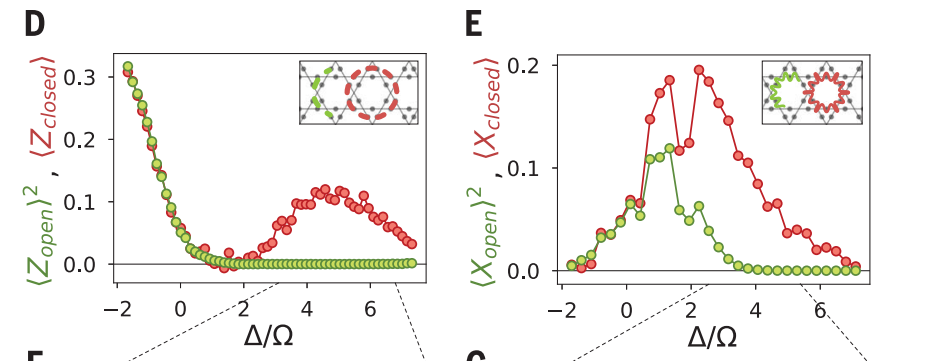
  既然实验上不能测磁序，就不得不考虑指数级数量的VBS态的共同几何特征。Z与X都是可测的，因为是封闭的loop，大量取平均可以得到Z与X的信息。而且对于$\Omega$与$\Delta$之比在3-5之间，Z与X都是非零的。在另一方面，我们取这些loop的时候截取这个loop的某一段，形成了一段开放的loop,如果计算这些loop的Z与X的数值，会发现这些均值为零，来源就是体系缺失的部分loop导致的拓扑序破坏。更精确的定义为：$Z_{open}/Z_{closed}^{0.5}$均值为零。关键的问题是我们逻辑到现在理解这个值为零是在VBS态下面理解，也就是说这个值为零是QSL态的一个判据。从下面两张图中可以看到在$\Omega$与$\Delta$之比在3-5区间，QSL态确实出现了。

  使用拓扑不变量来理解QSL态是近年来的一个前沿，这篇文章就作为一个例证。

REF

[1] Antiferromagnetism. The Triangular Ising Net, G.H.Wannier, Phys. Rev. 79, 357(1950).
[2] 《Interacting Electrons and Quantum Magnetism》Assa Auerbach，Springer New York, NY (2012).
[3] Quantum spin liquid states. Yi Zhou, Kazushi Kanoda, and Tai-Kai Ng. Rev. Mod. Phys. 89, 025003 (2017).
[4]Probing topological spin liquids on a programmable quantum simulator, G. Semeghin et al., Science374, 1242-1247 (2021).

PDF Download